Non-technical explanation of encryption and digital signatures

Having a basic understanding of encryption and digital signatures has become important as history has repeatedly taught us that we can’t trust everyone on the Internet (e.g. Internet service providers, email services etc.). This blog post will try to explain in a non-technical way how encryption and digital signatures work and why something called “private keys” are important to keep secret!

Symmetric encryption

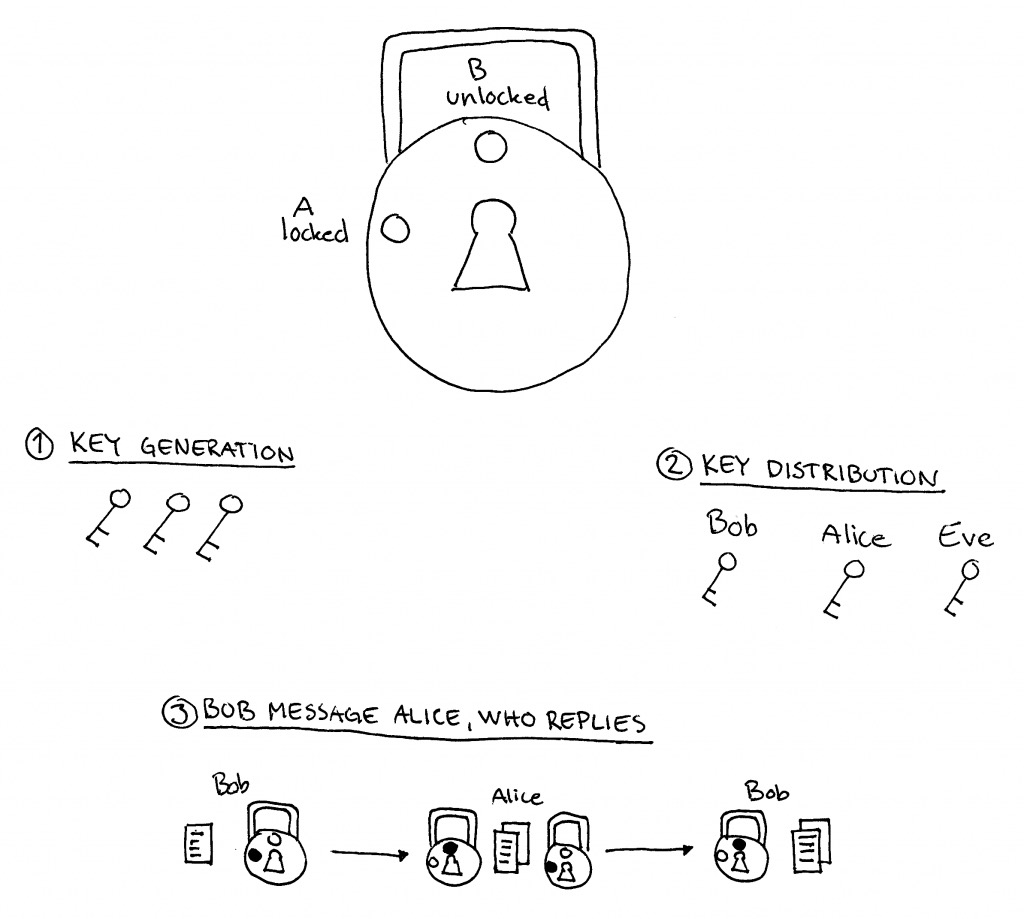
The most secure encryption is based on asymmetric encryption. But to understand that I first need to explain what symmetric encryption is. This can easily be explained with a message being delivered in a box which is secured with a regular lock. Each party exchanging the message possesses copies of the same key.

Bob locks the message in a box and sends it to Alice who can unlock the box and read the message. Alice can repeat this process in order to reply. The problem with this type of encryption is that the key that keeps the message secure is shared. If Eve got a copy of the key then she can read the message between Bob and Alice either while the message is in transit (e.g. on the same open WiFi) or if she finds a copy of the encrypted message after the fact (e.g. breaking into a server).

Symmetric encryption is the most common form of encryption online. For example, Facebook Messenger uses a form of symmetric encryption where Facebook keeps a copy of the shared key. This is why Facebook is able to read all your messages.

Asymmetric encryption

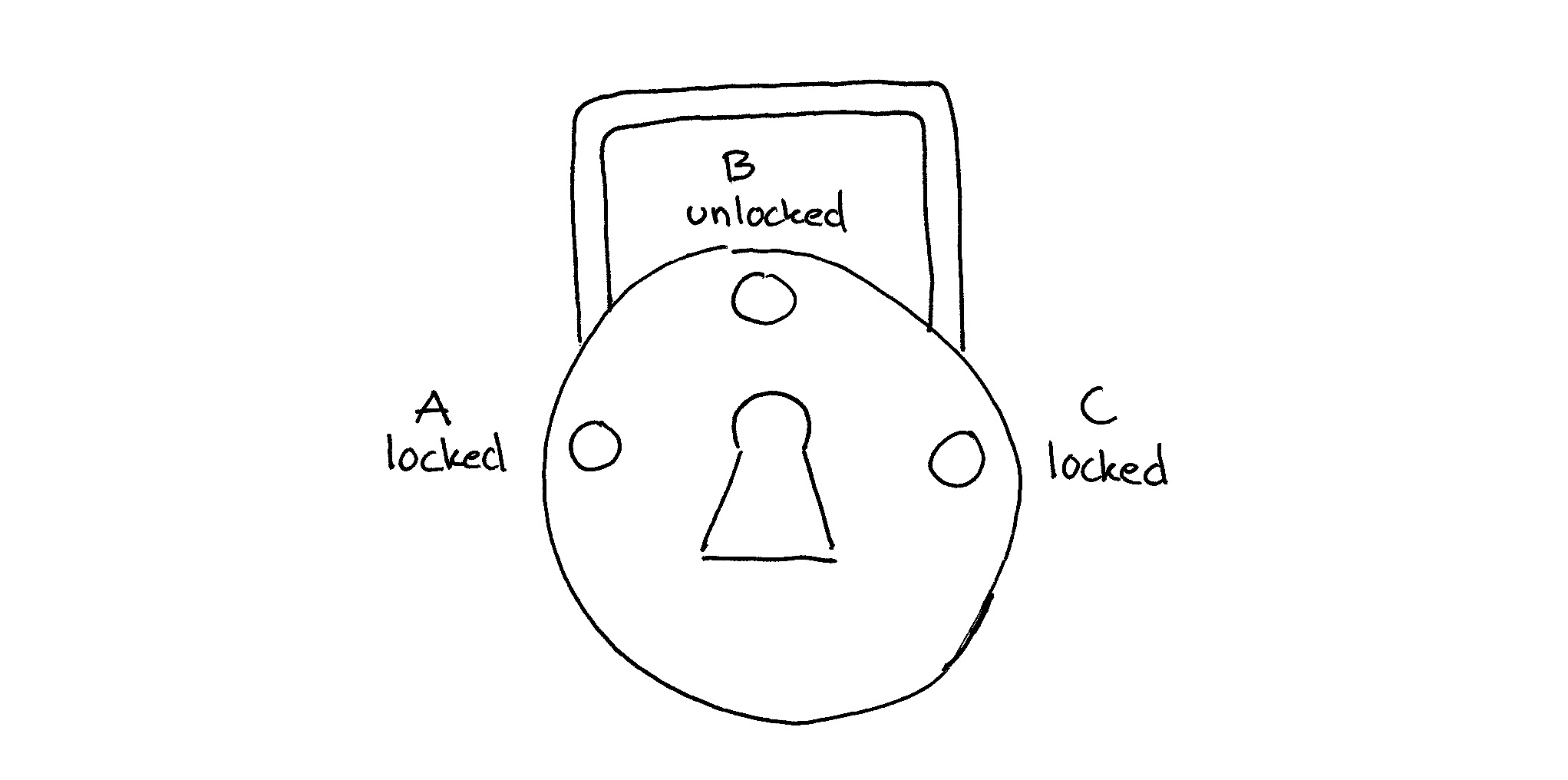
Notice the difference between the keys and locks.

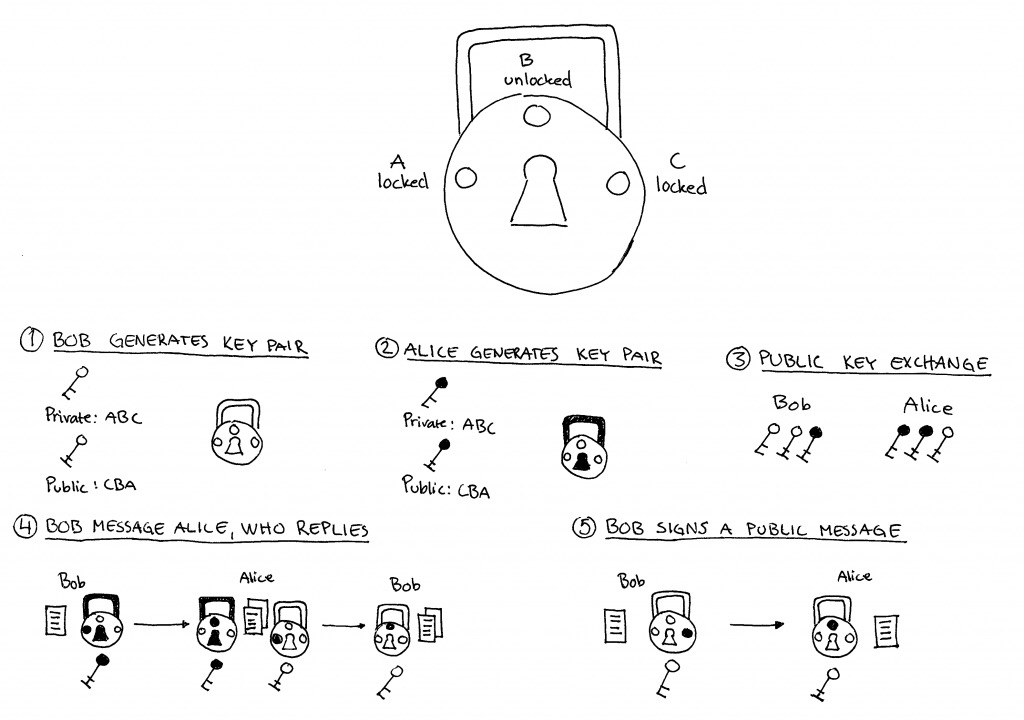
With asymmetric encryption we use a special lock with three states — A (locked), B (unlocked) and C (locked). For this lock there are two separate keys — the first key can only turn clockwise (from A to B to C) and the second key can only turn anti-clockwise (from C to B to A).

Alice keeps the first key privately for herself. The second key she can distribute publicly with whoever she wants to exchange private messages. She could even attach this public key to her business card.

If Bob wants to send Alice a message, he will put the message in a box and lock it with Alice’s public key (which can only turn anti-clockwise) to position A. The only key that can unlock this message is Alice’s private key (which can only turn clockwise). This model is much better because the key that keeps the message secure is not shared and therefore much harder to copy or steal.

The only true end-to-end encryption where one other than the sender and receiver is able to read the message is when asymmetric encryption is used and where you are in control of the private key. Don’t let anyone try to convince you that a conversation is private unless you control the private key.

Digital signatures

Another very useful feature with asymmetric encryption is digital signatures. If Bob wants to sign a public message (proving he was actually the one signing it) he will put this public message in a box and lock it with his private key (which can only turn clockwise) to position C. Anyone can verify if the message is authentic by unlocking it using Bob’s public key (which can only turn anti-clockwise) from position C to B. The act of unlocking the message is the proof of authenticity because the only key who could have put the lock into position C is Bob’s private key that he keeps for himself.

Math instead of locks

Of course digital encryption does not use physical locks in practice. Instead, mathematical formulas are used to create problems that are easy to solve one way (i.e. finding the public key) but practically impossible to reverse without some external knowledge (i.e. finding the private key). I say practically impossible because it’s theoretically possible to reverse these mathematical problems but since it involves finding very large prime numbers it would take longer than the age of the universe to find one.

Credit goes to Panayotis Vryonis for the original description of this concept.